快速自动分化（FAD）是另一种方式，除了众所周知的象征和有限差分方法计算函数的导数。虽然并不像这两个流行，基金会可以很好地补充他们。它专门定义为任何你喜欢的编程语言编写的代码片段只是功能上的分化。
在这里，我想概括这种方法的好处和我自己的实现FAD的算法描述在C。
FAD的，可以有助于在你的程序中嵌入分化能力。你不会真的需要知道，它是如何工作有效地使用它。 （还是你应该知道什么区别，以及如何可以使用函数的导数。）这种方法，真正的亮点，当你需要区分反复或递归定义一个函数，或者如果各自的代码片段包含分行等。
有一个优秀的在CodeProject上就如何实施象征性的分化。它也包含一些符号约定和分化公式为有用的功能，所以我不会在这里重复。
DY / DX表示X（一个偏导数，如果y还取决于其他参数比X）Y的衍生工具。{A2}
有只有两件事情你需要知道了解如何自动分化。幸运的是，他们是很容易理解。 （虽然，我再说一遍，他们是不是绝对必要的可以使用FAD的）第一个是sonbsp;所谓"链规则"的分化。
假设我们有一个复合函数y（X）= F（G（X））和g（x）和F（T）在x == X0和g（X0）微。那么Y也是微在x == X0及其衍生
DY / DX = df / dt的* DG / DX，
DG / DX计算为x == X0，df / dt的为t ==克（X0）。如果反过来，G（）函数是复合材料（例如G（X）= H（K（X））），我们可以应用此规则"的衍生产品链"一再延长，直到我们得到的功能，是不是复合（"基本功能"）:
DY / DX = df / dt的DH /杜* DK / DX，其中x == X0，T == G（X0），U == K（X0）。请注意，F（），H（）和K（）函数是"小学"（如SIN，COS，EXP等），所以我们已经知道确切的公式及其衍生物。
这个规则可以是广义多个参数的功能。稍微复杂的公式在这种情况下，但原理是相同的。
现在回想一下，许多经营浮点值的计算过程都超过一些复合功能的评价。各自的方案，对于一个给定的输入数据一样，执行"小学"行动的一个有限序列， - ，*，/，罪过，COS，棕褐色，EXP，日志等的结论是简单明了。如果我们能处理像一个复合函数这个序列，我们将能够计算及其衍生物，无论它有多长。快速自动分化正是这么做的。 （见{A3}更多详细的审查。近年来，已经有这个问题上的许多出版物。FAD的背后的想法是真的不新。）
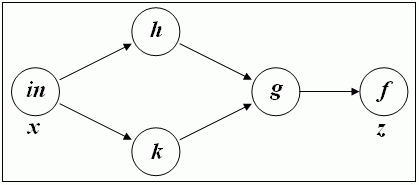
几个FAD的算法需要进一步处理以某种方式存储这个序列，其他算法不。持这种序列的一个最流行的数据结构是一个"计算图"（第二件事，重要的是要了解以上所述与连锁规则FAD）。在计算图形（CG）的节点对应的基本操作，而弧连接这些行动与他们的论据。见下面的一个样本函数的CG图Z（X）= F（G（H（X），K（X）））。 （"中"是指任何输入操作。）
{S0}
如果代码片段包含分支，循环，递归等，CG可针对不同的输入不同。这就是为什么企业管治是不是controlnbsp;流图或抽象语法树（AST）或类似。
自动微分算法计算点于同一功能的衍生工具的功能是评估（与符号的方法）。一旦CG已记录可以遍历从参数到自己感兴趣的功能（例如以上，即从X到Z"向前"）（"反向"）或以相反的方向来计算的衍生工具。因此，FAD的算法两大类，即"前进"和"反向"。
"正向"时尚，计算每一个给定在一个企业管治遍历参数的函数的导数。 （虽然一些前瞻性的算法不需要企业管治，以实际存储。）
"反向"时尚，计算一个给定的功能在一个企业管治的遍历整个梯度（与尊重每一个独立的变量的衍生工具）。处理了很多争论，每个功能的少数时，这可以是有益的。这种功能可以出现，例如，在矩阵操作等。
"前进"般的FAD的算法也可以被用来估计的计算过程中积累的函数值的不准确。正如你可能知道，用有限的相对精度浮点值通常存储。例如，1.0（1.0 1.0E - 16）存储为符合IEEE标准的双精度浮点数，通常被认为是相同的。这些"舍入误差积累，并导致一些计算值的不确定性。舍入误差估计算法（稀土）估计，这些不确定性（使用方法类似间隔演算）。{A4}
一个共同的方式来实现在C FAD的算法是使用特殊的"主动变"类的重载运算符和函数。 （有其他的方法，当然，这些方法的一些严重依赖解析，这实在是超出了本文的范围，人们可以找到{A5}这些方法的一些信息。）
考虑下面的代码片段:

    double x0, y0;

    double x, y, f;

    // get x0 and y0 from somewhere (ask the user, for example)

    //... 



    x = x0;    // initialize the arguments (x and y)

    y = y0;

    f = sin(y * cos(x));

为了聘用你需要改变感兴趣的变量的类型（X，Y和F）从双CADouble（"双积极"）是一种时尚库提供的FAD的算法。您还需要标记一个活跃的代码段（片段定义函数加以区别，其参数的初始化沿）的开始和结束。然后你得到以下几点:{C}
这些代码片段看上去非常相似，没有他们呢？在这两种情况下f（X，Y）的计算，但在第二个适当的顺序（CG）的基本操作也被记录下来。重心后计算F（）的衍生物，这样，可用于:

    double out_x, out_y;    // here the derivative values will be stored



    // compute df/dx partial derivative using forward mode FAD

    as.forward(x, f, out_x);



    // compute df/dy partial derivative using forward mode FAD

    as.forward(y, f, out_y);

有用的运算符和函数重载CADouble实例，因此，这些行动不仅做他们通常是，但也记录自己在企业管治。
就是这样。在你的代码变化不大，你嵌入的分化能力。当然，有没有免费的午餐。使用FAD可以减缓执行受影响的代码片段由2 400（甚至更多的FAD的算法，硬件等）的一个因素。遍历一个大的CG涉及大量的内存访问操作，当然可以，不是简单地执行数学运算的顺序慢。

请注意，不需要实际存储的CG（所谓的"快进"和"快速稀土元素"的算法）的方法通常是更快，需要较少的内存。{A6}
"里德图书馆"我已经写的规定如下:类为活跃的变量和活跃的部分;基于CG - FAD的方法:正向和反向（一个双值的一个或多个参数的双值函数的计算第一阶导数）;舍入误差估计（REE）的企业管治为基础的方法;实现"快进"的分化方法的"快速稀土元素"的算法，不需要企业管治;一些实用的东西（CG缓存，更新为新的参数值不重建的重心，如果可能的话，更多）。
（"励"是为"舍入错误的估计和分化"的缩写。它翻出来，稀土功能是在我工作的强制性，而使用FAD的似乎是可选的。为什么稀土在这个名字第一名是。 FAD的帮助也很大我不止一次虽然。）
你可以找到在所提供的{A7}生成的文档（见/ / DOC / reednbsp芦苇; librarynbsp; v01.chm）的类和方法的详细参考。在这里，我将只提及要点。

库​​中的有用的东西大部​​分驻留在命名空间中的芦苇目前支持的基本操作是:算术运算（， - ，*，/），以及像=联合作战，-=，*=，/ =;FMIN（X，Y）和fmax（X，Y）NBSP最小和最大的两个值（X和Y）;有条件的转让（condAssign（X，Y）== y如果x为正，否则为0）;ABS（X） - x的绝对值;SIN（X），COS（X），谭（X）;EXP（X），日志（X）;SQRT（X）。这种操作可以在未来的扩展。
上述操作的几个不是处处可微（如ABS（X）没有在x == 0的衍生）。在这些点进行评估时，仍然会计算一些值时，系统会不会崩溃，但当然，这个值不能被信任。 （也许我会作出这样的一个标志，或表明在未来的版本中这个条件。不幸的是，我现在没有这个时间。）
（;，LT; ==，GT等）关系操作也重载CADouble和CADoubleFamp; LT ...放大器; GT。在企业管治为基础的方法，它们是用来检测是否管治结构必须改变为新值的论点。在"快"的方法，他们简单地返回各自的浮点值的比较结果。
一个活跃的变量的值可通过的setValue（）和getValue（）方法。
实例芦苇:CADouble类可以创建内外活跃的部分。 （出于效率的考虑），但你可以分配的东西给他们，并使用重载的操作，他们只在一个活跃的部分。不这样做将导致在调试模式下的断言和释放不确定的行为。
我选择创建一个固定大小的物体的特殊速度远远超过使用默认的new和delete的内存分配器，的存储皮质颗粒。芦苇/ mem_pool.h。人们可以找到} {A8的信息，如分配器，例如。
所有CG - FAD的算法作为芦苇的方法实现:CActiveSection类。其中包括:

INT（CADouble参数，CADouble功能，doubleamp;）;
计算使用转发模式FAD和返回出结果的参数arg的函数func衍生。返回值是微不足道的。

INT的反向（CADouble参数，CADouble功能，doubleamp;）
是否相同的，如上述使用反向模式。
INT ree_lower（STD::vectorlt; CADoublegt;放大器;参数，性病:vectorlt; doublegt;放大器; ERR）;计算错误的估计。默认参数应该存储与机床精度（即约1.1E - 16的相对精度为符合IEEE标准的正常化的双重价值。）您可以通过设置参数的变量的初始绝对误差值覆盖。这些值是通过ERR载体。 ree_lower（）返回后，您可以检索任何通过CADouble变量的累积误差值::getAcc（）方法，例如双E = f.getAcc（）

可以用这些方法的其他重载版本。请参阅文件和与这篇文章有关详细信息，所提供的例子。
要使用这些方法，你应该在你的代码的＃include芦苇/ adouble.h和芦苇/ asection.h和芦苇/ LIB / reed.lib库（或一个调试版本reed_d.lib）链接你的项目。见提供的例子（"简单"，"国际热核实验堆"和"梯度"）。
"快速"前进和稀土元素算法在芦苇/ adouble_f.h实施。您不需要任何积极的部分或CG使用这些。你也不需要reed.lib。只要在您的项目＃包括芦苇/ adouble_f.h util.cpp添加到它，你都设置。 "iter_f"的例子说明如何使用这些"快"的算法。{A9}
正如我上面提到的的，您可以使用FAD的算法（CG基于"快"的版本）来区分迭代定义的函数，用树枝等所提供的功能是在兴趣点微功能。考虑下面的例子（见"iter_f"从与一个完整的实施例子的ZIP存档的项目）。假设Y = Y（x）的定义是这样的:

    double x0 = ...; // set the argument value or ask the user for it

    size_t m = ...;     // Number of iterations to perform. Let the user define it too.

    

    // Note: the value of m can be unknown at the compile-time. FAD will handle this.



    double x, y;

    x = x0; //argument

    y = x;

    for (size_t i = 0; i < m; i++)

    {

        if (y < 0.5)

        {

            y = 4.0 * y * (1.0 - y);

        }

        else if (y > 0.5)

        {

            y = 1.0 - 0.75 * y * y;

        }

        else

        {

            y = -1.0;

            std::cout << "1/2 has been hit!\n";    // shouldn't get here

            break;

        }

    }

需要计算在x == X0 DY / DX吗？没有问题。由此产生的代码片段使用"快速"前进方法，但你可以使用企业管治为基础的方法。如上所述更改的类型，设置初始的衍生工具的价值（DX / DX == 1.0），你会得到

    double x0 = ...; // set the argument value or ask the user for it

    size_t m = ...;     // Number of iterations to perform. Let the user define it too.



    CADoubleFF x, y; // for REE use CADoubleRee instead.

    // Active sections are not necessary for "fast forward" and "fast REE"

    // algorithms because these algorithms do not require CG to be stored.



    x = x0; //argument

    x.setAcc(1.0);    // Accumulated derivative is 1.0 in x (dx/dx). By default it is zero.



    y = x;

    for (size_t i = 0; i < m; i++)

    {

        if (y < 0.5)

        {

            y = 4.0 * y * (1.0 - y);

        }

        else if (y > 0.5)

        {

            y = 1.0 - 0.75 * y * y;

        }

        else

        {

            y = -1.0;

            std::cout << "1/2 has been hit!\n";    // shouldn't get here

            break;

        }

    }

衍生DY / DX的值将被计算与y（X）在x == X0。然后，您可以通过y.getAcc（）和y.getValue（）检索这些值，分别为。很简单，是不是？{A10}
"FADcpp_examples"Visualnbsp Studio解决方案中包含5个项目。这是根据MSnbsp测试的Visual C 7.1只。 （也许它不会工作在6.0或更早，由于我用一些模板技巧，我没有测试6.0虽然它。）
"FADcpp_examples /芦苇"目录中包含"芦苇库"本身（代码和文档）。您可以使用"reed_lib"这一解决方案的项目重建库。
其他4个项目中使用该库的例子:"简单"的 - 一个简单的例子。计算的衍生工具，F =单（Y * COS（X）），X和Y由用户提供。同时使用正向和反向的企业管治为基础的算法。太演示稀土元素。还演示了如何重用现有的CG在另一点来计算的衍生工具（如果可能）。
"国际热核实验堆"。区分迭代定义的函数（见上文）。的参数和迭代次数由用户提供。
"iter_f"。同为"国际热核实验堆"，除了"快"前锋和稀土元素算法被用来代替企业管治为基础的。
"梯度"。计算二次函数的梯度，F（X）=（X * AX），其中A是一个3x3矩阵，X =（X0，X1，X2），采用反向FAD的算法。只有一个单一的CG遍历是在这种情况下使用。 （如果被雇用前向算法，这将需要3 CG遍历）。{A11}
这篇文章是一个所谓的快速自动分化（FAD）的轮廓。 FAD的，当您需要嵌入分化能力，在你的程序和/或分行处理功能，可以帮助循环递归等方式自动分化可以补充象征性的分化。后者主要用于当我们有一个区别函数的公式（"封闭的"）。如果我们不这样做，往往可以帮助FAD的。希望我的快速自动分化和舍入误差估计算法的实施，将证明对你有用。
试试看吧！任何反馈将不胜感激。{A12}{A13}自动分化和舍入误差估计的历史。自动微分算法:理论，实施和应用，A. Griewank和GFCorliss， EDS，暹罗，宾夕法尼亚州费城，1991年。。{A14}{A15}高效的C性能的编程技术。艾迪生韦斯利，1999年。 {A16}v.0.1本文的第一个版本和的例子都可用。