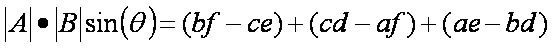一个C#中的向量类型
 简介
简介
,多年来,我所看到的人与矢量数学斗争。本指南应通过创建一个可重用的Vector3类型和它背后的数学的步行。后固定3仅仅指的是在3维的向量(X,Y,Z)。
代码没有设计成快速或有效的,但要尽可能简单和理解。为此,作为个人喜好,Vector3类型是挤满了相关的功能和多个接口的方法(如静态和非静态方法的变种)。很多人会认为这个臃肿的代码,但是,我认为,它使代码的程序员友好。显然,成长,我会倾向于重构功能的退了出去,因为我创建对象和类型的功能更好地适应作为一个项目。我看到,实现最大程度的凝聚力和减少耦合和依赖。
我已经用在三维直角坐标系(即三个垂直的X,Y和Z轴)和欧几里德几何。不要担心这些条款,他们只是在高中所涉及的一些数学的正式名称。向量空间体积(立方体);注意,您可以使用其他的向量空间,如一个圆柱形的空间,一轴(通常Z)与圆柱的半径。
你可能已经猜到,电脑是相当缓慢的,这种类型的数学。矩阵数学,更有效,但更难理解。您将需要一个三角和代数的基本掌握,了解本指南。
除非另有说明,我假设的矢量位置,在点(0,0,0)的。替代位置向量,单位向量,这可以解释为没有数量或无限幅度和载体对载体的起源是另一个载体,幅度正在从原点向量的距离。
请注意,本指南非常详细,似乎光顾经验丰富的C#程序员。请不要得罪了,我已经编写了广大观众的引导。
一个快速的词汇:运营商,这是用于定义一个操作,如加(符号)(AB)操作数,这些都是在操作使用的变量,如(a)及(b)在(AB)。左手侧(左轴)的操作数是(A),右手端(右轴)的操作数是(B)。
本指南中的所有方程假设(或V1)和B(或V2)可以分解成:
(A B C)=(D E F)= B使用代码
首先,让我们定义如何将存储矢量信息。我常常不创建结构时编码,但我们Vector3这是完美的。如果你正在读这篇文章,你可能已经知道,一个向量沿轴的数量代表的值。在本教程中,我们将开发一个立体型,所以... ...你的变量和三个轴。public struct Vector3
{
private double x, y, z;
}
是什么方向轴?从一个可视化的背景下,我总是假设:
{S0}
您可能已经注意到,Z是负你看不起轴。这是一种常见的约定,如OpenGL图形库。这将成为重要的考虑俯仰,滚转和偏航方法时。
快速分流:为什么一个结构,而不是一类?
struct和class之间的差别:而struct是值类型,而不是堆栈上创建,从而减少垃圾收集的开销。他们是按值传递的,而不是通过引用。他们快速,高效地创建和处理。你不能从中他们(即非继承)其他类型。
他们只是少数的成员(变量)的类型。微软建议一个结构应小于16个字节。您不需要新的关键字来实例化一个结构。
基本上,它的样子,行为像,是一个原始类型。虽然,没有向量类型为何不能创建一个类的原因。发展一个结构的缺点是,集合类。NET框架类铸铁结构。这意味着一个Vector3的大集合,将有一个高的铸造开销。
一个结构上更深入的文章已被写入由S. Senthil库马尔 访问变量
访问变量
你有没有注意到的变数是私人?
虽然我选择了建立一个结构,我习惯性地隐藏我的变量,并创建公共访问的mutator属性。这不是严格把好结构的做法,但我创造了他们的情况下,我觉得有必要在稍后的日期转换成一个类(这是好的做法,阶级结构)。
另外的属性,数组风格的界面,也提供了。这允许用户调用Vector3 myVector [X],myVector [Y],myVector [Z]。此外,用户可以获取或设置使用数组属性的数组中的所有组件,即myVector.Array = {X,Y,Z}。{C}
有物业还提供了访问和操作一个向量的大小。一个向量幅度(或绝对值),不论是它的长度方向,并且可以使用公式确定:
{S1}
SumComponentSquares法(以下使用),可以看到在本文的后面。请注意,幅度始终是积极的,不能设置一个向量(0,0,0)的幅度。public double Magnitude
{
get
{
return Math.Sqrt ( SumComponentSqrs() );
}
set
{
if (value < 0)
{ throw new ArgumentOutOfRangeException("value", value,
NEGATIVE_MAGNITUDE); }
if (this == origin)
{ throw new ArgumentException(ORAGIN_VECTOR_MAGNITUDE, "this"); }
this = this * (value / Magnitude);
}
}
private const string NEGATIVE_MAGNITUDE =
"The magnitude of a Vector must be a positive value, (i.e. greater than 0)";
private const string ORAGIN_VECTOR_MAGNITUDE =
"Cannot change the magnitude of Vector(0,0,0)";
构造类型,使用下面的构造方法已提供的典型的类语法:public Vector3(double x, double y, double z)
{
this.x = 0;
this.y = 0;
this.z = 0;
X = x;
Y = y;
Z = z;
}
public Vector3 (double[] xyz)
{
this.x = 0;
this.y = 0;
this.z = 0;
Array = xyz;
}
public Vector3(Vector3 v1)
{
this.x = 0;
this.y = 0;
this.z = 0;
X = v1.X;
Y = v1.Y;
Z = v1.Z;
}
您可能会奇怪,为什么我之前设置赋值X,Y和Z为0。一个结构不会允许访问之前的每个变量(小写的x,Y,Z),已初始化的属性(大写的X,Y,Z轴)。米莎#322; BRY#322;家评论说,这是不寻常,使用构造函数的属性赋值时。作为个人口味问题,我总是试图以这种方式使用的属性。它确保任何验证的代码写入到设定的方法是由构造救起。我觉得这是有利于维护代码时。在Vector3类型,因为它代表,有没有这样的问题在属性的验证,是学术。这两种范式将是有效的。操作符重载
我们现在有一个用于存储,访问和变异的Vector3及其组成部分(X,Y,Z)的框架。现在,我们可以考虑适用于向量的数学运算。首先,让我们通过重载基本的数学运算符。
重载运算符允许程序员定义一个类型是如何在代码中使用。举个例子来说,加号运算符()。对于数字类型,这表明除了两个数字。对于字符串,它代表了两个字符串的连接。运算符重载是巨大的好处,程序员描述一个类型应该如何与系统交互时。在C#中的下列运算符可以被重载:此外,串联,并加固()减法和否定( - )逻辑非(!)按位求补(〜)增量()递减( - )布尔真理(真实)布尔值false(假)乘(*)司(/)除法的余数(%)逻辑AND(&)逻辑OR(|)逻辑异或(^)二进制左移(<<)二进制右移(GT,GT;)运营商平等,平等和不相等(==和!=)差异\比较运算符,小于和大于(LT和GT;)差异\比较运算符,小于或等于和大于或等于(<=和GT; =)此外(V3 = V1 V2)
另外两个向量是通过简单地增加了X,Y,和一个矢量的z分量(即XX,YY,ZZ)。public static Vector3 operator+(Vector3 v1, Vector3 v2)
{
return
(
new Vector3
(
v1.X + v2.X,
v1.Y + v2.Y,
v1.Z + v2.Z
)
);
}
两个向量的加减是简单的减法的X,Y,z分量和一个向量(即XX,YY,ZZ)。public static Vector3 operator-(Vector3 v1, Vector3 v2 )
{
return
(
new Vector3
(
v1.X - v2.X,
v1.Y - v2.Y,
v1.Z - v2.Z
)
);
}
否定一个向量反转其方向。这是通过简单地否定每个向量的组成部分。public static Vector3 operator-(Vector3 v1)
{
return
(
new Vector3
(
- v1.X,
- v1.Y,
- v1.Z
)
);
}
向量的加固实际上什么也不做,但返回原向量加法规则(即- X - X和X = X)。public static Vector3 operator+(Vector3 v1)
{
return
(
new Vector3
(
+ v1.X,
+ v1.Y,
+ v1.Z
)
);
}
当比较两个向量,我们使用的大小(之前看到的)。小于(结果= V1 public static bool operator<(Vector3 v1, Vector3 v2)
{
return v1.Magnitude < v2.Magnitude;
}
欠大于或等于的比较两个向量,则返回true,仅在左手侧的向量(V1)的幅度小于其他(V2)或两个幅度相等的幅度。public static bool operator<=(Vector3 v1, Vector3 v2)
{
return v1.Magnitude <= v2.Magnitude;
}
大于比较两个向量,则返回true,仅在左手侧的向量(V1)的幅度大于其他的幅度(V2)。public static bool operator>(Vector3 v1, Vector3 v2)
{
return v1.Magnitude > v2.Magnitude;
}
大于或等于比较两个向量,则返回true,只有左手端向量(V1)的幅度大于其他的幅度(V2)或两个幅度相等。平等(结果= V1 == V2)
要检查,如果两个向量是相等的,我们只是检查组件对。我们和结果,使任何一对不等于将导致错误。public static bool operator==(Vector3 v1, Vector3 v2)
{
return
(
(v1.X == v2.X)&&
(v1.Y == v2.Y)&&
(v1.Z == v2.Z)
);
}
有在这个阈值时使用的计算平等的文章的意见很多讨论。从存储小数(即浮动,双,和十进制变量)的精度问题茎的需要。我个人同意用红色男爵谁建议:{BR }"...你不应该实现代码内的公差值。
什么是一个适合这种宽容的价值呢?
这是问题... ..."
然而,妥协的我已经实现平等宽容作为一个可以设置为零(忽略)常数。public static bool operator==(Vector3 v1, Vector3 v2)
{
return
(
Math.Abs(v1.X - v2.X) <= EqualityTolerence &&
Math.Abs(v1.Y - v2.Y) <= EqualityTolerence &&
Math.Abs(v1.Z - v2.Z) <= EqualityTolerence
);
}
public const double EqualityTolerence = Double.Epsilon;
你应该现在发现,下面的代码产生:
1号线:假
2号线:真static void Main(string[] args)
{
Vector3 vect = new Vector3(1, 2, 3);
Vector3 vect2 = new Vector3(1, 2, 3.000000000000001);
Vector3 vect3 = new Vector3(1, 2, 3.0000000000000001);
Console.WriteLine(vect == vect2);
Console.WriteLine(vect == vect3);
Console.ReadKey();
}
如果被重载的运算符==(等于),C#的力量,以覆盖!=(不等于)。这简直是平等的倒数。public static bool operator!=(Vector3 v1, Vector3 v2)
{
return !(v1==v2);
}
由一个标量(如2)的矢量司是通过除以除数(S2)的每一个组成部分。public static Vector3 operator/(Vector3 v1, double s2)
{
return
(
new Vector3
(
v1.X / s2,
v1.Y / s2,
v1.Z / s2
)
);
}
向量的乘法是棘手的。有三种不同类型的矢量乘法:一个标量乘法(V3 = V1 * S2)点产品(S3 = V1,V2)交叉产品(V3 = V1 * V2)
只有乘法标和标司已实现运算符重载。我所看到的运营商,如〜点的产品,以区别于跨产品的重载;我相信,这可能会导致混乱和选择不提供点和跨产品,让用户调用相应的方法,而不是运营商。
标量乘法实现乘以每个组成部分的标量值。public static Vector3 operator*(Vector3 v1, double s2)
{
return
(
new Vector3
(
v1.X * s2,
v1.Y * s2,
v1.Z * s2
)
);
}
乘法的操作数的顺序可以颠倒,这是被可交换。public static Vector3 operator*(double s1, Vector3 v2)
{
return v2 * s1;
}
两个向量跨产品产生一个给定的两个向量平面的正常。
{S2}
这个公式(其中V1 =和v2 = B)
{S3}
{S4}的
{五}
这个方程总是产生一个向量结果。
THETA的正弦是用来核算矢量的方向。西塔始终把A和B之间(即 )最小的角度。
)最小的角度。
该公式的右边是在扩大和简化的左侧,使用规则:黄大仙
0??= 0
仙90??= 1
在矩阵式符号,这看起来像:
{七}
,你应该知道这个公式是可交换非。这意味着,跨产品的V1 V2是V2跨产品V1相同。
这一切的C#代码:
在可能的情况下,我已经创建了延长程序员的选项时,使用类型的静态方法。这直接影响或影响的实例的方法,简单地调用的静态方法。由于这样的实例对应的静态方法是:public Vector3 CrossProduct(Vector3 other)
{
return CrossProduct(this, other);
}
注意实例方法,这并不影响从它被调用,但返回一个新的Vector3对象实例。我之所以选择来实施这种方式的原因有两个跨产品之一,以点产品它可以不产生一个向量,和两个,因为跨产品是通常用来产生其他地方使用一个正常的,在原Vector3需要保持一致要保持不变。
[附注]手动计算两个向量的交叉产品的快速模板:

两个向量的点积是一个标量值的公式定义;
{S3}


方程应该总是产生一个标结果。
余弦THETA是考虑到矢量的方向。西塔始终把A和B(即 )之间的最小角度。
)之间的最小角度。
该公式的右边是在扩大和简化的左侧,使用规则:
COS 0??= 1
COS 90??= 0
这在C#代码:public static double DotProduct(Vector3 v1, Vector3 v2)
{
return
(
v1.X * v2.X +
v1.Y * v2.Y +
v1.Z * v2.Z
);
}
和它的:public double DotProduct(Vector3 other)
{
return DotProduct(this, other);
}
我们现在有一个Vector3类型所需的所有基本功能。为了使这种类型的真正有用的,我已经提供了额外的功能。正常化和单位向量
单位向量1级。如果要测试向量是单位向量,我们只需检查对已经定义的幅度方法1。public static bool IsUnitVector(Vector3 v1)
{
return v1.Magnitude == 1;
}
public bool IsUnitVector()
{
return IsUnitVector(this);
}
改变相等(==)运算符允许一个门槛,我们必须做相同的静态IsUnitVector方法(实例方法不变):public static bool IsUnitVector(Vector3 v1)
{
return Math.Abs(v1.Magnitude -1) <= EqualityTolerence;
}
规范化是一些单位向量的向量转换的过程。这个公式是:

public static Vector3 Normalize(Vector3 v1)
{
// Check for divide by zero errors
if ( v1.Magnitude == 0 )
{
throw new DivideByZeroException( NORMALIZE_0 );
}
else
{
// find the inverse of the vectors magnitude
double inverse = 1 / v1.Magnitude;
return
(
new Vector3
(
// multiply each component by the inverse of the magnitude
v1.X * inverse,
v1.Y * inverse,
v1.Z * inverse
)
);
}
}
public void Normalize()
{
this = Normalize(this);
}
private const string NORMALIZE_0 = "Can not normalize a vector when" +
"it's magnitude is zero";
正常化的实例方法直接影响的实例。插值
这种方法需要从两个向量之间的插补值。这种方法需要三个参数,一个起点(矢量V1),终点(矢量V2),和一个控制这是1和0之间的一小部分。 V1和V2之间的一点是采取控制决定。控制为0,将返回V1和V2控制将返回1。

N = N1(1 - T)n2t
或
n的= N1吨(N2 - N1)
N = N1 TN2 - TN1
或:

其中:
N =当前值
N1 =初始值(V1)
N2 =终值(V2)
T =控制参数, 和
和 ,
,
public static Vector3 Interpolate(Vector3 v1, Vector3 v2, double control)
{
if (control >1 || control <0)
{
// Error message includes information about the actual value of the
// argument
throw new ArgumentOutOfRangeException
(
"control",
control,
INTERPOLATION_RANGE + "\n" + ARGUMENT_VALUE + control
);
}
else
{
return
(
new Vector3
(
v1.X * (1-control) + v2.X * control,
v1.Y * (1-control) + v2.Y * control,
v1.Z * (1-control) + v2.Z * control
)
);
}
}
public Vector3 Interpolate(Vector3 other, double control)
{
return Interpolate(this, other, control);
}
private const string INTERPOLATION_RANGE = "Control parameter must be a" +
"value between 0 & 1";
这种方法发现使用毕达哥拉斯定理的两个位置向量之间的距离。

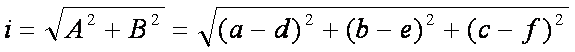
public static double Distance(Vector3 v1, Vector3 v2)
{
return
(
Math.Sqrt
(
(v1.X - v2.X) * (v1.X - v2.X) +
(v1.Y - v2.Y) * (v1.Y - v2.Y) +
(v1.Z - v2.Z) * (v1.Z - v2.Z)
)
);
}
public double Distance(Vector3 other)
{
return Distance(this, other);
}
向量的绝对值是它的大小。 ABS的方法提供了帮助程序员谁不知道这两个功能是相同的的,并提供一个静态接口的规模经营者。public static Double Abs(Vector3 v1)
{
return v1.Magnitude;
}
</implementation />
public double Abs()
{
return this.Magnitude;
}
这种方法发现正常化和点产品使用两个向量之间的角度。




^指归一(单位)向量
| |指向量的大小。public static double Angle(Vector3 v1, Vector3 v2)
{
return
(
Math.Acos
(
Normalize(v1).DotProduct(Normalize(v2))
)
);
}
public double Angle(Vector3 other)
{
return Angle(this, other);
}
这些方法比较两个向量幅度,分别返回向量的最大或最小的幅度。public static Vector3 Max(Vector3 v1, Vector3 v2)
{
if (v1 >= v2){return v1;}
return v2;
}
public Vector3 Max(Vector3 other)
{
return Max(this, other);
}
public static Vector3 Min(Vector3 v1, Vector3 v2)
{
if (v1 <= v2){return v1;}
return v2;
}
public Vector3 Min(Vector3 other)
{
return Min(this, other);
}
欧拉旋转围绕轴X,Y,Z分别使用方法俯仰,偏航和滚动。

Eric__评论说,他所期望的不同的配置。{BR }"...横滚,俯仰和偏航是指飞机的议案的概念。
这是标准的符号X是(鼻子),Y是右翼和Z是(向水平飞行的地球)
因此它遵循,辊是关于X积极的,间距是积极的,绕Y(沥青手段爬上)和偏航是积极围绕Z(积极偏航时,飞机机头移动到右)。"
为了说明他的观点考虑如下图:
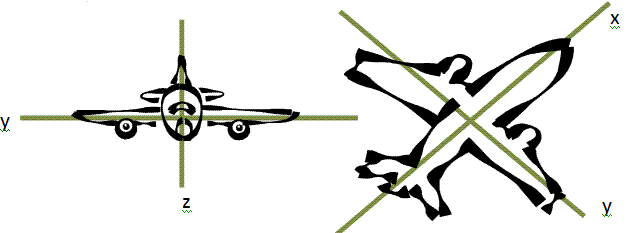
这似乎完全合理。它!但只有当考虑单一的飞机对象。当我们考虑虚拟场景与多个对象(例如电脑游戏或虚拟现实环境),所有的对象必须是有关他们的用户感知。虚拟场景的标准轴Z轴往下看用户。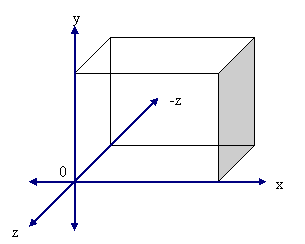
所以到飞机的例子,它极有可能,我们将以下的飞机,因为它进入现场苍蝇:
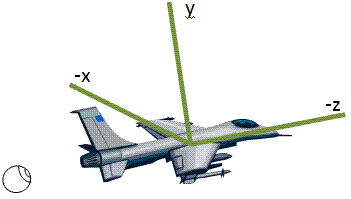
我们希望,这解释了为什么所述轴和俯仰,偏航,辊配置。音高
这种方法绕X轴的向量旋转一个度(欧拉绕X旋转)。
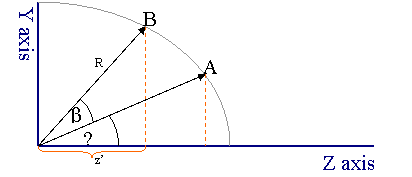
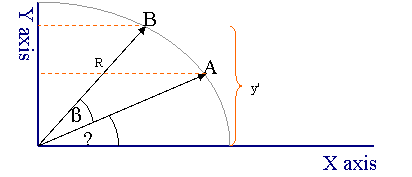











斜边(R)取消方程。public static Vector3 Pitch(Vector3 v1, double degree)
{
double x = v1.X;
double y = ( v1.Y * Math.Cos(degree) ) - ( v1.Z * Math.Sin(degree) );
double z = ( v1.Y * Math.Sin(degree) ) + ( v1.Z * Math.Cos(degree) );
return new Vector3(x, y, z);
}
public void Pitch(double degree)
{
this = Pitch(this, degree);
}
这个方法直接影响到该方法被称为实例。偏航
这种方法绕Y轴的向量旋转一个度(欧拉绕Y旋转)。
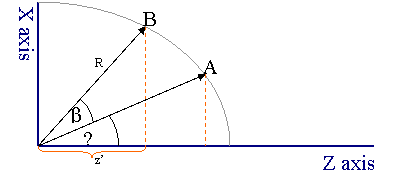












斜边(R)取消方程。public static Vector3 Yaw(Vector3 v1, double degree)
{
double x = ( v1.Z * Math.Sin(degree) ) + ( v1.X * Math.Cos(degree) );
double y = v1.Y;
double z = ( v1.Z * Math.Cos(degree) ) - ( v1.X * Math.Sin(degree) );
return new Vector(x, y, z);
}
public void Yaw(double degree)
{
this = Yaw(this, degree);
}
这个方法直接影响到该方法被称为实例。滚
这个方法旋转一个度(欧拉围绕Z轴旋转)绕Z轴的矢量。
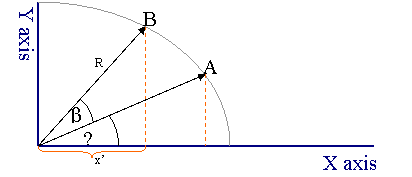












斜边(R)取消方程。public static Vector3 Roll(Vector3 v1, double degree)
{
double x = ( v1.X * Math.Cos(degree) ) - ( v1.Y * Math.Sin(degree) );
double y = ( v1.X * Math.Sin(degree) ) + ( v1.Y * Math.Cos(degree) );
double z = v1.Z;
return new Vector3(x, y, z);
}
public void Roll(double degree)
{
this = Roll(this, degree);
}
这个方法直接影响到该方法被称为实例。背面
这种方法解释为面对正常的载体,并确定是否正常代表一个背对着飞机行的视线向量。一个背对着飞机将是无形的,在渲染场景,这样,可以从许多场景计算除外。

 如果
如果 ,然后
,然后
 如果
如果 ,然后
,然后

public static bool IsBackFace(Vector3 normal, Vector3 lineOfSight)
{
return normal.DotProduct(lineOfSight) < 0;
}
public bool IsBackFace(Vector3 lineOfSight)
{
return IsBackFace(this, lineOfSight);
}
此方法检查,如果两个向量垂直(即如果一个向量是正常的)。public static bool IsPerpendicular(Vector3 v1, Vector3 v2)
{
return v1.DotProduct(v2) == 0;
}
public bool IsPerpendicular(Vector3 other)
{
return IsPerpendicular(this, other);
}
此方法的代码提供了米莎#322; BRY#322;家。该方法计算的三个向量的标量三重积。这是一个平行六面体的几何形状的体积。更多信息可在 。这种方法是可交换非的。
。这种方法是可交换非的。public static double MixedProduct(Vector3 v1, Vector3 v2, Vector3 v3)
{
return DotProduct(CrossProduct(v1, v2), v3);
}
public double MixedProduct(Vector3 other_v1, Vector3 other_v2)
{
return DotProduct(CrossProduct(this, other_v1), other_v2);
}
我提供了一个目标向量组件的功能。这些都是作为一个整体的向量数学上并不有效。例如,有没有一个向量提高电源(据我所知),但是PowComponents方法可以用来提高每到一个给定的功率的X,Y,Z的概念。萨姆组件
这种方法简单相加的矢量分量(X,Y,Z)。public static double SumComponents(Vector3 v1)
{
return (v1.X + v1.Y + v1.Z);
}
public double SumComponents()
{
return SumComponents(this);
}
这种方法给定的功率乘以向量的组件。public static Vector3 PowComponents(Vector3 v1, double power)
{
return
(
new Vector
(
Math.Pow(v1.X, power),
Math.Pow(v1.Y, power),
Math.Pow(v1.Z, power)
)
);
}
public void PowComponents(double power)
{
this = PowComponents(this, power);
}
这种方法适用于每个向量组件的平方根函数。广场
这种方法广场每个向量的组件。
public static Vector3 SqrComponents(Vector3 v1)
{
return
(
new Vector3
(
v1.X * v1.X,
v1.Y * v1.Y,
v1.Z * v1.Z
)
);
}
public void SqrComponents()
{
this = SqrtComponents(this);
}
该方法找到每个向量组件平方的总和。public static double SumComponentSqrs(Vector3 v1)
{
Vector3 v2 = SqrComponents(v1);
return v2.SumComponents();
}
public double SumComponentSqrs()
{
return SumComponentSqrs(this);
}
为了完整的标准化方法已添加完整的类型。这些实现IComparable,IComparablelt; Vector3gt,IEquatablelt; Vector3gt,IFormattable。
的方法来获取一个类型的文字描述和实现IFormattable。
VerbString提供了详细的文字描述。的ToString可以接受数字格式字符串进行选择一个字符x,Y或Z表示有关矢量分量来形容。public string ToVerbString()
{
string output = null;
if (IsUnitVector())
{
output += UNIT_VECTOR;
}
else
{
output += POSITIONAL_VECTOR;
}
output += string.Format("( x={0}, y={1}, z={2})", X, Y, Z);
output += MAGNITUDE + Magnitude;
return output;
}
private const string UNIT_VECTOR =
"Unit vector composing of ";
private const string POSITIONAL_VECTOR =
"Positional vector composing of ";
private const string MAGNITUDE =
" of magnitude ";
public string ToString(string format, IFormatProvider formatProvider)
{
// If no format is passed
if (format == null || format == "")
return String.Format("({0}, {1}, {2})", X, Y, Z);
char firstChar = format[0];
string remainder = null;
if (format.Length > 1)
remainder = format.Substring(1);
switch (firstChar)
{
case 'x':
return X.ToString(remainder, formatProvider);
case 'y':
return Y.ToString(remainder, formatProvider);
case 'z':
return Z.ToString(remainder, formatProvider);
default:
return
String.Format
(
"({0}, {1}, {2})",
X.ToString(format, formatProvider),
Y.ToString(format, formatProvider),
Z.ToString(format, formatProvider)
);
}
}
public override string ToString()
{
return ToString(null, null);
}
要产生一个系统使用的哈希代码(需要,以实现比较操作(即==,!=)):public override int GetHashCode()
{
return
(
(int)((X + Y + Z) % Int32.MaxValue)
);
}
检查相等(==操作符的标准化版本)和实施IEquatablelt; Vector3gt;public override bool Equals(object other)
{
// Check object other is a Vector3 object
if(other is Vector3)
{
// Convert object to Vector3
Vector3 otherVector = (Vector3)other;
// Check for equality
return otherVector == this;
}
else
{
return false;
}
}
public bool Equals(Vector3 other)
{
return other == this;
}
两个向量,它返回的比较方法:-1,如果幅度不到别人的幅度0如果值等于其他的幅度1,如果幅度大于其他的幅度
这使得Vector类型实现IComparable和IComparablelt; Vector3gt;接口。Public int CompareTo(object other)
{
if(other is Vector3)
{
Vector3 otherVector = (Vector3)other;
if( this < otherVector ) { return -1; }
else if( this > otherVector ) { return 1; }
return 0;
}
else
{
// Error condition: other is not a Vector object
throw new ArgumentException
(
// Error message includes information about the actual type of the
// argument
NON_VECTOR_COMPARISON + "\n" + ARGUMENT_TYPE +
other.GetType().ToString(),
"other"
);
}
}
public int CompareTo(Vector3 other)
{
if (this < other)
{
return -1;
}
else if (this > other)
{
return 1;
}
return 0;
}
private const string NON_VECTOR_COMPARISON =
"Cannot compare a Vector to a non-Vector";
private const string ARGUMENT_TYPE =
"The argument provided is a type of ";
最后四个标准的矢量常量定义:public static readonly Vector3 origin = new Vector3(0,0,0);
public static readonly Vector3 xAxis = new Vector3(1,0,0);
public static readonly Vector3 yAxis = new Vector3(0,1,0);
public static readonly Vector3 zAxis = new Vector3(0,0,1);
和杂项的只读值:public static readonly Vector3 MinValue =
new Vector3(Double.MinValue, Double.MinValue, Double.MinValue);
public static readonly Vector3 MaxValue =
new Vector3(Double.MaxValue, Double.MaxValue, Double.MaxValue);
public static readonly Vector3 Epsilon =
new Vector3(Double.Epsilon, Double.Epsilon, Double.Epsilon);
Vector3实现了[Serializable]属性,因此可以被写入文件。我建议以下几点:static void Main(string[] args)
{
Vector3 vect = new Vector3(1, 2, 3);
XmlSerializer x = new XmlSerializer(vect.GetType());
x.Serialize
(
new System.IO.FileStream("test.xml", System.IO.FileMode.Create),
vect
);
}
产生一个XML文件,其中包含:<?xml version="1.0"?>
<Vector
xmlns:xsi="http://www.w3.org/2001/XMLSchema-instance"
xmlns:xsd="http://www.w3.org/2001/XMLSchema">
<X>1</X>
<Y>2</Y>
<Z>3</Z>
<Magnitude>3.7416573867739413</Magnitude>
</Vector>
我们现在有一个Vector3类型具有以下功能:
 构造函数Vector3(双X双Y,双ž)Vector3(双[] XYZ)Vector3(矢量V1)属性XŸž大小运营商此[]索引器 - ==!=*/LT;GT;LT; =
静态方法交叉积DotProductMixedProduct正常化IsUnitVector插距离ABS角最大闵偏航音高滚IsBackFaceIsPerpendicularSumComponentsSumComponentSqrsSqrComponentsSqrtComponentsPowComponents这直接影响到实例变量的实例方法正常化偏航音高滚SqrComponentsSqrtComponentsPowComponents返回一个新的对象或类型的实例方法交叉积DotProductMixedProductIsUnitVector插ABS角最大闵IsBackFaceIsPerpendicularSumComponentsSumComponentSqrs的CompareTo等于的ToStringGetHashCode的
只读和常量的值MaxValue的MINVALUEEPSILON原产地X轴ZAXIS兴趣点
构造函数Vector3(双X双Y,双ž)Vector3(双[] XYZ)Vector3(矢量V1)属性XŸž大小运营商此[]索引器 - ==!=*/LT;GT;LT; =
静态方法交叉积DotProductMixedProduct正常化IsUnitVector插距离ABS角最大闵偏航音高滚IsBackFaceIsPerpendicularSumComponentsSumComponentSqrsSqrComponentsSqrtComponentsPowComponents这直接影响到实例变量的实例方法正常化偏航音高滚SqrComponentsSqrtComponentsPowComponents返回一个新的对象或类型的实例方法交叉积DotProductMixedProductIsUnitVector插ABS角最大闵IsBackFaceIsPerpendicularSumComponentsSumComponentSqrs的CompareTo等于的ToStringGetHashCode的
只读和常量的值MaxValue的MINVALUEEPSILON原产地X轴ZAXIS兴趣点
有我在这篇文章,并提供源代码的发展中使用的资源的数量,我想确认以下内容: 项目 - 卢卡斯通孔Livschitz
项目 - 卢卡斯通孔Livschitz 项目 - 奔休斯敦计算机图形学的基本数学 - 约翰文斯(国际标准书号1-85233-380-4)历史
项目 - 奔休斯敦计算机图形学的基本数学 - 约翰文斯(国际标准书号1-85233-380-4)历史
到:方法,以反映有关给定的正常Vector3一个图形测试\演示应用程序变化:(V1.00 - V1.20)震级的方法是封装在propertiy不正确的序列化属性已被删除平等和IsUnitVector方法,允许的公差现在的Abs方法返回幅度通用IEquatable和IComparable接口已实施IFormattable接口已落实实施混合产品功能额外添加,并改名为基于组件的功能(如SumComponentSquares)矢量改名到Vector3